When Units Go Square

What is a Square Foot?

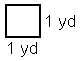
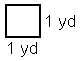
As you can see, each side is 1 yard long. So the total area of the square is 1x1 which is 1.

1 what?

It isn't one yard—that is the length of the side, but not the area of the square. The area of the square is "1 square yard." A square yard is a measurement of area and it can also be written as 1 yd² for reasons that should be obvious by the time I'm finished (but aren't now). A length can be measured in yards, never in square yards. An area can be measured in square yards, never in yards. So you cannot "convert" yards to square yards, because they measure fundamentally different things. Learning about square yards is really learning about area.

Let's look at another picture.

What is the area of this rectangle? 2 times 1/2: again it is 1, "1 square yard." So you now have a square and a rectangle which have no lengths in common, but the same area. That's a very strong statement. It means that if you covered these surfaces with marbles, it would take the same number of marbles to cover each surface. Many different shapes can all have the same "area" and it says something real about them.

OK, so each of these shapes is "1 square yard." How many square feet are they? There are three feet in a yard, so you might be tempted to say 3 square feet in a square yard, but you'd be wrong. The answer is 3², or 9. Let me demonstrate with another picture.

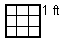
What I've done is divide our original square into three equal vertical strips, and three equal horizontal strips. Now, looking at this 3-by-3 thing I have just drawn, you can see two things.

First, you can see that if the original (whole square) was one yard on each side, then each smaller square is one foot on each side, because there are three feet in a yard.

Second, you can see that there are a total of 9 of these "square feet" inside the whole "square yard." This is the key moment I've been building up to this whole time, so please make sure that you can convince yourself of this: 9 square feet equals 1 square yard.

Now let's check your understanding. How many square inches are in a square foot? How many square centimeters in a square meter? Answer these questions for yourself, then click here to see my answers.

Dimensional Analysis with Square Units

For instance,

1 yard * 1 yard = 1 yard²

This is the first calculation we did, to find the area of a 1x1 square. Now, you can see that just as the numbers multiply (1*1=1), so do the units (yard*yard=yard²). When we did the same calculation in feet, we found that

3 ft * 3 ft = 9 ft²

Again, the numbers multiply (3*3=9) and so do the units (ft*ft=ft²).

But how about converting? In my paper I talk about multiplying things by "1 yard/3 ft" to do a conversion. Supposing you do that twice? Then you're multiplying by

(1 yard/3 ft) (1 yard/3 ft) = (1 yard²) / (9 ft²)

...which makes sense, since we already said, there are 9 ft² in 1 yard².

So if someone asked you to convert 5 square yards to square feet, you would know that the answer is:

5 yards² * (9 ft² / 1 yard²) = 45 ft²

...and so on.

Send comments or questions to the author