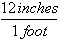 or
or 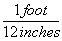
Copyright (c) 1996 by Kenny Felder
The above examples are for units of length, but there are many other things that we measure, and all of them require units. For instance, time can be measured in seconds or minutes (or hours, or days, etc); angles can be measured in degrees or in radians; and so on. Some units are made up of other units: for instance, you might measure the speed of a car in miles/hour. So "50 mi/hr" means that every hour, the car travels 50 miles; very different from a car travelling 50 mi/s, for instance! No matter what you are measuring, you must specify the units in order to give a measurement.
Obviously, you cannot find the answer to this question by adding 60 to 6. The reason is that the two figures are given in different units. Before you can add the two numbers, you have to convert one of them to the units of the other. Then, when you have two numbers in the same units, you can add them.
In order to perform this conversion, you need a conversion factor. That is, in this case, you have to know how many inches make up a foot. You probably already know the answer: 12 inches is 1 foot. So knowing that, you can perform the calculation in two steps as follows:
a) 60 inches is really 60/12 = 5 feet
b) 5 feet + 6 feet = 11 feet
The second half of the calculation is easy; once all your units are the same, calculation is a snap. The tricky part is the conversion: because sometimes you have to divide, and sometimes you have to multiply. In the above example, I converted from inches to feet by dividing by 12. If I were going the other way, converting from feet to inches, I would have multiplied by 12. How do I figure out which to do?
One way is by using common sense. I know that 60 inches can't possibly be 720 feet; there have to be less feet than inches, obviously. However, sometimes common sense falls down on you. For instance, if you want to convert miles/hour into meters/second, what you do you multiply or divide by what?
Fortunately, there is another way: relatively easy once you get used to it, and guaranteed to work in every situation. This technique goes by the somewhat intimidating name of dimensional analysis, and I apologize. I didn't name it.
First of all, we write our conversion factor as a fraction. 12 inches = 1 foot, so the conversion factor is
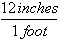 or
or 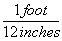
Because 12 inches is the same thing as 1 foot, that fraction is just like 5/5; it's equal to 1. And we can multiply by it without changing anything.
So, let's try that on our 60 inches.
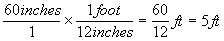
The critical thing to note about the above equation is that the units behave like numbers do when you multiply fractions. That is, the inches on top and the inches on the bottom cancel out, leaving feet. Then all you have to worry about is the numbers.
Suppose that I had written in the wrong way, like the following.
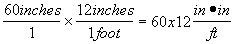 (Wrong)
(Wrong)
I would have immediately realized that multiplying 60 * 12 is wrong, because the units of the answer are inches*inches/feet instead of just feet. So the dimensional analysis shows me immediately that dividing is correct, and multiplying is not.
Such conversions are even easier in the metric system, of course, since all the conversion factors are multiples of ten. For intstance, to convert 10 km to m, you would simply write
10 km * 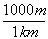 = 10,000 m
= 10,000 m
At this point, you may well be asking yourself "so what?" Dimensional analysis doesn't take much time, and it isn't very difficult, but it is certainly more trouble than the common-sense method.
To answer that, let's look at a more difficult unit conversion problem. Suppose that I want to convert 55 mi/hr into m/s. I know that 1 mile is 5280 feet, that 1 meter is 3.3 feet, that 1 hour is 60 minutes, and that 1 minute is 60 seconds. Now, what do I multiply, or divide, by what?
This is a very tricky question, but using dimensional analysis, it becomes a snap. First of all, I write all the above conversions as fractions, remembering that I might have to turn some of them upside-down.
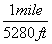 *
* 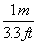 *
* 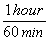 *
* 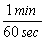
Now I write out an equation to convert from miles/hour to m/s, watching the units to make sure they cancel.
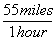 *
* 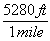 *
* 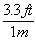 *
* 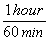 *
* 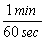 =
= 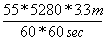 (Wrong)
(Wrong)
Did you follow that, and make sure that the units cancel to give us meters/second? If you did, you hopefully were not surprised by the annotation on the right: because this equation is most definitely incorrect. Do you see why? The "feet" on the top of the fractions don't cancel; so instead of being left with meters/seconds, we are left with the rather ungainly units of 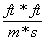 . That is most definitely not what we are looking for; which is a perfect example of how, in a complicated problem like this, dimensional analysis can prevent you from making errors. If we turn the feet/meters fraction around, we get:
. That is most definitely not what we are looking for; which is a perfect example of how, in a complicated problem like this, dimensional analysis can prevent you from making errors. If we turn the feet/meters fraction around, we get:
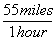 *
* 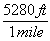 *
* 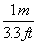 *
* 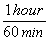 *
* 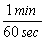 =
= 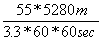 = 24.4 m/s.
= 24.4 m/s.
If you think that was overly difficult, try to imagine what it would have been like without dimensional analysis! You would still have had to multiple the 55, 5280, 3.3, 60, and 60, but first you would have had to figure out which to multiply and divide. And if you had made a mistake, how would you have caught yourself?
Although the formalism of dimensional analysis (not to mention the name) can be intimidating at first, you will find that once you have worked a few problems, it's a snap. Try it!
Or you can go to www.onlineunitconversion.com to check your answers with a spiffy online conversion tool!
 Gary and Kenny Felder's Math and Physics Help Home Page
Gary and Kenny Felder's Math and Physics Help Home Page
www.felderbooks.com/papers
 Send comments or questions to the author
Send comments or questions to the author