

Next: Power-Law Expansion
Up: Scale Factor Evolution
Previous: The Scale Factor Equation
Correcting for Staggered Leapfrog
In practice the program uses a staggered leapfrog algorithm so in
solving for 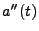 the value of
the value of 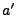 is known at
is known at  where
where 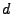 is the time step. See section 6.4 for more details. The
solution to this problem is to use the two equations
is the time step. See section 6.4 for more details. The
solution to this problem is to use the two equations
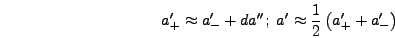 |
(6.27) |
where  and
and  refer to the values of
refer to the values of 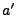 at
at 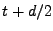 and
and
 respectively and all other variables are evaluated at time
respectively and all other variables are evaluated at time
 . Take the evolution equation to be
. Take the evolution equation to be
 |
(6.28) |
Plugging this form into equation (6.27) and eliminating
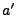 gives
gives
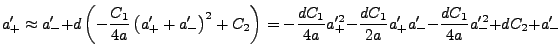 |
(6.29) |
To determine whether to use the plus or minus sign in equation
(6.31) consider the limit as
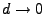 . In this limit
. In this limit
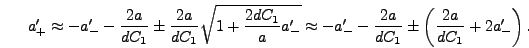 |
(6.32) |
This suggests that the plus sign must be used in order to reduce to
the limit
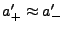 . Hence
. Hence
 |
(6.33) |
In the program it's useful to calculate 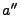 , which is roughly
, which is roughly
 , so
, so
![\begin{displaymath}
a'' \approx {1 \over d} \left[-2 a_-' - {2 a \over d C_1}\le...
...{2 d C_1 a_-' \over a} + {d^2 C_1 C_2 \over
a}}\right)\right].
\end{displaymath}](img274.png) |
(6.34) |
Thus equation (6.26) becomes
![\begin{displaymath}
a'' \approx {1 \over d}\left\{-2 a_-' - {2 a \over d C_1} \l...
...a_{pr} f_{i,pr}\vert^2 +
a^{C_4} V_{pr}\right)}\right]\right\}
\end{displaymath}](img275.png) |
(6.35) |
where
 |
(6.36) |


Next: Power-Law Expansion
Up: Scale Factor Evolution
Previous: The Scale Factor Equation
Go to The
LATTICEEASY Home Page
Go to Gary Felder's Home
Page
Send email to Gary Felder at gfelder@email.smith.edu
Send
email to Igor Tkachev at Igor.Tkachev@cern.ch
This
documentation was generated on 2008-01-21
![]() the value of
the value of ![]() is known at
is known at ![]() where
where ![]() is the time step. See section 6.4 for more details. The
solution to this problem is to use the two equations
is the time step. See section 6.4 for more details. The
solution to this problem is to use the two equations
![\begin{displaymath}
a'' \approx {1 \over d} \left[-2 a_-' - {2 a \over d C_1}\le...
...{2 d C_1 a_-' \over a} + {d^2 C_1 C_2 \over
a}}\right)\right].
\end{displaymath}](img274.png)
![\begin{displaymath}
a'' \approx {1 \over d}\left\{-2 a_-' - {2 a \over d C_1} \l...
...a_{pr} f_{i,pr}\vert^2 +
a^{C_4} V_{pr}\right)}\right]\right\}
\end{displaymath}](img275.png)