

Next: Conformal Coordinates
Up: Definitions of Number and
Previous: Definitions of Number and
The ordinary Fourier transform of a field 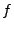 is defined as
is defined as
 |
(5.5) |
The problem with using this definition for a classical scalar
field is that if the Fourier components 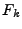 are given fixed
values the resultant field values
are given fixed
values the resultant field values  become dependent on the
overall size of the box within which the theory is defined. For
example
become dependent on the
overall size of the box within which the theory is defined. For
example
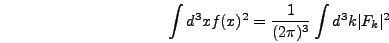 |
(5.6) |
which implies
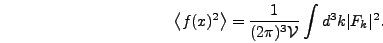 |
(5.7) |
The size of the box does not affect the integral, except by
turning it into a discrete sum. So to keep  (and by
extension all intensive quantities) independent of the box size we
define a modified Fourier transform
(and by
extension all intensive quantities) independent of the box size we
define a modified Fourier transform
 |
(5.8) |
where 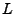 is the size of the box. This modified transform takes on
the same value regardless of the box size, while the actual
Fourier transform must be rescaled. Note that the units of
is the size of the box. This modified transform takes on
the same value regardless of the box size, while the actual
Fourier transform must be rescaled. Note that the units of 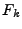 are
are ![$[M]^{-2}$](img144.png) while those of
while those of  are
are ![$[M]^{-1/2}$](img146.png) .
.
The Fourier transform used by the program is neither of these,
however, but rather the discrete Fourier transform 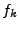 , related
to the usual, continuous, one by
, related
to the usual, continuous, one by
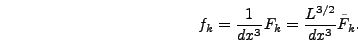 |
(5.9) |
All physical quantities should be defined in terms of
 and the Fourier transform
and the Fourier transform 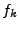 used by the program
should be adjusted accordingly. For example, the initial vacuum
state
used by the program
should be adjusted accordingly. For example, the initial vacuum
state
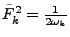 becomes
becomes
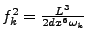 . See section 6.3.2 for more
details.
. See section 6.3.2 for more
details.


Next: Conformal Coordinates
Up: Definitions of Number and
Previous: Definitions of Number and
Go to The
LATTICEEASY Home Page
Go to Gary Felder's Home
Page
Send email to Gary Felder at gfelder@email.smith.edu
Send
email to Igor Tkachev at Igor.Tkachev@cern.ch
This
documentation was generated on 2008-01-21
![]() is defined as
is defined as
![]() , related
to the usual, continuous, one by
, related
to the usual, continuous, one by