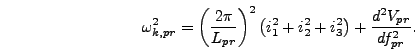

Next: Initial Conditions for Field
Up: Initial Conditions on the
Previous: Homogeneous Field and Derivative
Initial Conditions for Field Fluctuations
Although the field equations are solved in configuration space with
each lattice point representing a position in space, the initial
conditions are set in momentum space and then Fourier transformed to
give the initial values of the fields and their derivatives at each
grid point. As mentioned above, all of the expressions in this and the following two sections will be derived for a three dimensional lattice. Section 6.3.5 will explain how the results are altered in other dimensions. The Fourier transform 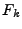 in three dimensions is defined by
in three dimensions is defined by
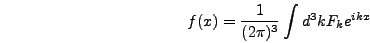 |
(6.50) |
It is assumed that no significant particle production has occurred
before the beginning of the program, so quantum vacuum fluctuations
are used for setting the initial values of the modes. The
probability distribution for the ground state of a real scalar field in a FRW
universe is given by [1,2]
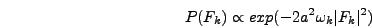 |
(6.51) |
where
 |
(6.52) |
 |
(6.53) |
Although 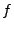 is a real field the Fourier transform is of course
complex, so this probability distribution is over the complex
plane. The phase of
is a real field the Fourier transform is of course
complex, so this probability distribution is over the complex
plane. The phase of 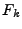 is uniformly randomly distributed and the
magnitude is distributed according to the Rayleigh distribution
is uniformly randomly distributed and the
magnitude is distributed according to the Rayleigh distribution
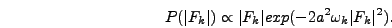 |
(6.54) |
Note that this distribution gives the mean-squared value
 |
(6.55) |
To derive the expressions used for setting field values on the lattice
we must modify equation (6.54) to account for a finite,
discrete space, then account for the rescalings of field and spacetime
variables, and finally discuss how to implement the Rayleigh
distribution. In the rest of this section we do each of these in turn.
There are two steps involved in normalizing these modes on a finite,
discrete lattice. First this definition has to be adjusted to account
for the finite size of the box. This is necessary in order to keep the
field values in position space independent of the box size. To see
this consider the spatial average 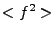 .
.
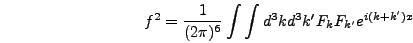 |
(6.56) |
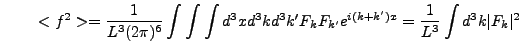 |
(6.57) |
where  is the volume of the region of integration. So in
order to keep
is the volume of the region of integration. So in
order to keep 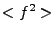 constant as
constant as 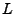 is changed the modes
is changed the modes
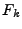 must scale as
must scale as 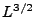 .
.
Accounting for the discretization of the lattice is even easier.
From the definition of a discrete Fourier transform (denoted here
as 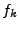 ) in three dimensions
) in three dimensions
 |
(6.58) |
Note that values such as 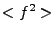 will be affected by changes
in the lattice spacing, but this is reasonable since this spacing
determines the ultraviolet cutoff of the theory. Without such a
cutoff
will be affected by changes
in the lattice spacing, but this is reasonable since this spacing
determines the ultraviolet cutoff of the theory. Without such a
cutoff 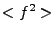 would be divergent.
would be divergent.
Putting these effects together gives us the following expression for
the rms magnitudes, which we denote by 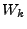 .
.
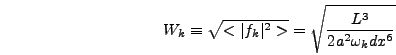 |
(6.59) |
At a point  on the Fourier transformed lattice the
value of
on the Fourier transformed lattice the
value of 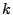 is given by
is given by
 |
(6.60) |
Next we rescale to program variables. The 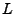 ,
, 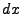 , and
, and 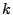 rescalings are determined by the rescaling of
rescalings are determined by the rescaling of 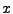 in equation
(6.2), i.e.
in equation
(6.2), i.e.
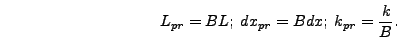 |
(6.61) |
We can define a rescaling
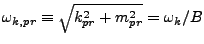 where
where
 . (The
extra factor of
. (The
extra factor of 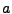 appears because the bare values
appears because the bare values 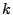 and
and 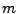 are
measured in conformal and physical units respectively.) Then, taking
into account the field rescaling
are
measured in conformal and physical units respectively.) Then, taking
into account the field rescaling
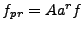
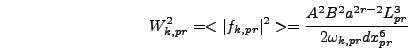 |
(6.62) |
Meanwhile the rescaled mass is given by
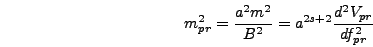 |
(6.63) |
Finally it remains to implement the Rayleigh distribution
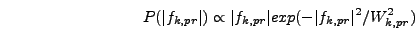 |
(6.64) |
Normalizing this distribution gives
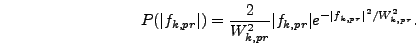 |
(6.65) |
To generate this distribution from a uniform deviate (i.e. a random
number generated with uniform probability between 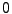 and
and 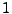 ) first
integrate it and then take the inverse (see [3]), which gives
) first
integrate it and then take the inverse (see [3]), which gives
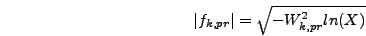 |
(6.66) |
where 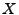 is a uniform deviate.
is a uniform deviate.
There are two more points to note in setting the initial conditions
for the fluctuations. The first is simply that the scale factor is set
to 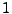 at the beginning of the calculations and may thus be dropped
from the equations. The second is that the phases of all modes are
random and uncorrelated, so they are each set randomly. The
expression for the field modes is thus
at the beginning of the calculations and may thus be dropped
from the equations. The second is that the phases of all modes are
random and uncorrelated, so they are each set randomly. The
expression for the field modes is thus
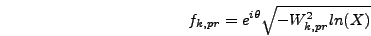 |
(6.67) |
where
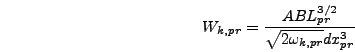 |
(6.68) |
and 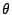 is set randomly between
is set randomly between 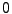 and
and 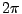 . The frequency
. The frequency
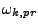 for a given point
for a given point  on the momentum
space lattice is given by
on the momentum
space lattice is given by
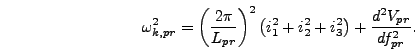 |
(6.69) |


Next: Initial Conditions for Field
Up: Initial Conditions on the
Previous: Homogeneous Field and Derivative
Go to The
LATTICEEASY Home Page
Go to Gary Felder's Home
Page
Send email to Gary Felder at gfelder@email.smith.edu
Send
email to Igor Tkachev at Igor.Tkachev@cern.ch
This
documentation was generated on 2008-01-21
![]() in three dimensions is defined by
in three dimensions is defined by
![]() .
.
![]() ) in three dimensions
) in three dimensions
![]() .
.
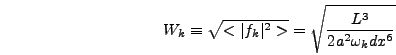
![]() on the Fourier transformed lattice the
value of
on the Fourier transformed lattice the
value of ![]() is given by
is given by
![]() ,
, ![]() , and
, and ![]() rescalings are determined by the rescaling of
rescalings are determined by the rescaling of ![]() in equation
(6.2), i.e.
in equation
(6.2), i.e.
![]() at the beginning of the calculations and may thus be dropped
from the equations. The second is that the phases of all modes are
random and uncorrelated, so they are each set randomly. The
expression for the field modes is thus
at the beginning of the calculations and may thus be dropped
from the equations. The second is that the phases of all modes are
random and uncorrelated, so they are each set randomly. The
expression for the field modes is thus