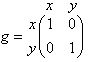
To see what that means, consider that to describe the motion of an object it's necessary to use a set of coordinates. For example I can say that a ball moved five units in the y-direction. Since the laws of physics describe how objects move, those laws are typically formulated in a way that depends on the type of coordinate system being used. A set of coordinates used to label all points in space and time is called a reference frame. For example, Newton's second law relates the motion of an object (specifically its acceleration) to the forces acting on it. This relationship will not be valid in a rotating reference frame, however. More specifically, Newton's laws are only valid in a special class of coordinate systems known as inertial reference frames.
I should note at this point that most people familiar with basic physics don't think of a reference frame in terms of coordinate labels, but rather as the point of view of a particular observer. This latter viewpoint, while useful for building intuition in many situations, is not well-defined in general. For the rest of the paper I will drop the phrase "reference frame" in favor of the more precise one: "coordinate system."
It is as a description of physics in arbitrary coordinate systems that GR is most clearly seen to be a generalization of Einstein's special theory of relativity. Special relativity (SR) is a modification of Newton's laws, but like those laws it is only valid in a very special set of coordinate systems. Once again we define an inertial coordinate system as any coordinate system in which the laws of SR apply. If you use a different coordinate system, for example one that's accelerating relative to an inertial one, then you must use GR instead. The mathematical formalism of GR, which describes the curved spacetimes that result from gravity, also applies to flat spacetime (no gravity) if that spacetime is being described in a non-standard coordinate system, such as one that's accelerated or rotating relative to an inertial one.
I can summarize all three of these pictures—the two discussed in the previous paper and this new one about coordinate systems—into a unified statement of what GR is about. I'll simply state it briefly here and spend the rest of the paper explaining this unified statement more clearly. Special relativity is our most accurate theory describing how objects move when you neglect gravity and describe spacetime using an inertial coordinate system. GR is a generalization of those laws that applies to any coordinate system. Without gravity, however, you can always find an appropriate coordinate transformation that will bring you to an inertial coordinate system. When gravity is present the same laws of GR can be used. In this case, however, there is no coordinate transformation that can make the coordinate system inertial. A spacetime that can not be described by an inertial coordinate system is called a curved spacetime. GR provides a mathematical way of describing the intrinsic, coordinate-free properties of a spacetime. Finally, GR tells you how those properties will be determined as a function of the matter inside the spacetime. In the words of John Wheeler: "Matter tells space how to curve, and space tells matter how to move."
The rest of this paper will explain in more detail what it means for GR to be a theory of physics in arbitrary coordinates and how one goes about formulating laws in such a theory. I begin by reviewing how the laws of physics are formulated in Newtonian mechanics and in SR, with particular attention paid to the role of coordinate systems in these theories. Then I describe how GR generalizes this description by formulating laws valid in any coordinate system. Having presented the basic ideas of the theory, I then discuss the Big Bang Model as an example of how to apply these ideas to a particular situation.
My expectation is that you will get the most out of this paper if you read it twice. This introduction lays out some of the basic ideas, but in a way that is probably too general to give you a clear idea of what they mean. The following sections describe the general ideas behind the theory of GR in a much more careful way. Nonetheless, it may be hard to follow them without seeing an explicit example of how they work. The example presented at the end should hopefully clarify those ideas. Having gone through that example, you might then be in a much better position to reread the previous sections and understand better how these ideas work in practice.
At several points in the text are suggested exercises that may help you to get a feel for some of the ideas being presented. Since I'm assuming you have studied some physics by this point, I will also assume that you have learned enough about your own learning style to judge how these exercises will work best for you. If you want my advice, though, I would suggest just thinking about most of the exercises on a first reading so as not to break the flow of the text. On a second reading you could then do some or all of them to solidify your new, deep understanding of the physics of GR. To help you quickly recognize these problems I have marked them all in bold, red type, like so.
In principle there is an infinite number of ways I could assign coordinates to spacetime. For example, if I had a set of coordinates I could define a new one by redefining the origin, or defining a set that is moving relative to my first set, or perhaps one that is spinning around relative to the first set. How do I decide which if any of these coordinate systems are the best ones to use for doing physics? The answer is that Newton's three laws of motion will only work in a subset of the possible coordinate systems. We call the coordinate systems for which Newton's laws hold valid inertial. If you define a set of coordinates for spacetime and find that Newton's laws hold valid using those coordinates, you have selected an inertial coordinate system.
Once you've defined such a coordinate system, you can use it to predict the motions of any particles, provided you know the forces acting on them. Moreover, you can then predict their behavior in any coordinate system. To do so you first solve for their motion in your inertial system using Newton's laws and then you transform the result into the new coordinate system. You can even generalize this procedure so that rather than finding paths of particular particles in the new coordinates, you can formulate general laws of physics for these coordinates.
For instance suppose you define a new coordinate system such that x, y,and t are the same for each point as they are for your inertial system, while the third spatial coordinate is assigned a new value z'=z+4t. (The number 4 here is a velocity measured in whatever units your coordinate system uses, e.g. 4 m/s.) This new set of labels defines a coordinate system in constant motion relative to your original inertial one. What do Newton's laws look like in this new coordinate system? Consider F=ma. Force, as determined by the various force laws (gravity, electricity, etc.), won't change in the new coordinate system. To relate the acceleration in the two systems we note that d2x'/dt2 = d2x/dt2, d2y'/dt2 = d2y/dt2, d2z'/dt2 = d2z/dt2. So for any object we consider both F and a will be the same in the new coordinate system as they were in the old one. You can likewise confirm that Newton's first and third laws are unchanged in the new system, so we can conclude that our new coordinate system is inertial. Any coordinate system related to an inertial one by a transformation of the type z'=z+vt will also be inertial.
Suppose, however, that you choose instead to define a coordinate system that is accelerating relative to your old one: x'=x, y'=y, z'=z+3t2. Once again the forces given by Newton's law of gravity or Coulomb's law will remain the same, as will acceleration in the x and y directions. In the z direction, however, d2z'/dt2 = d2z/dt2+6. We know that m(d2z/dt2)=F, so in terms of the new coordinates we can write m (d2z'/dt2) = F—6m. The simplest interpretation of this law is that in this coordinate system all particles experience an acceleration due to normal forces such as gravity and electricity plus an additional constant force of -6m in the z' direction. In general you will find that most coordinate transformations you can define will give rise to extra terms like this in Newton's second law. Such extra terms are called "fictitious forces." As an exercise, consider starting in an inertial coordinate system and defining a new system where z'=z+t3. What are the fictitious forces in this new system?
Before leaving Newtonian physics behind, I want to make an important comment about the term "fictitious forces." The implication of this name is that the correct description of physics is the inertial one and all other descriptions are simply mathematical fictions. In Newtonian physics this conclusion seems quite natural. Surely a system in which F=ma is better than a system in which F+F'=ma where F is the sum of forces from all other particles and F' is an arbitrary force acting on everything all the time. Nonetheless it's important to keep in mind that this conclusion is not ultimately defensible. If I want to maintain that the fundamental laws of physics are those that describe what I see from the surface of the Earth, which rotates relative to an inertial system, I am free to do so. If you wish to refute me and say that the fundamental laws are really the ones that describe what you see floating freely in space, the only argument you will be able to make is that your laws are simpler and more elegant than mine. I make this point now—and I urge you to think it over carefully—because it's useful to have this fact in mind when we get to GR where there are no inertial systems and no coordinate-dependent set of laws has any obvious claim to being the most fundamental.
SR is very much like Newtonian mechanics in certain ways. Like Newtonian mechanics, SR gives you a set of laws for predicting the motions of particles subject to arbitrary forces. As with Newtonian mechanics, these laws are only valid in a special class of coordinate systems, which are still known as inertial coordinate systems. There are essentially two differences between Newtonian mechanics and SR. The first is that the laws of SR are more complicated. For example they predict that when you accelerate an object from rest it will contract, and that an arbitrarily large force can never accelerate a particle above the speed of light. Complicated though they might be, however, you can write these laws down and once you have defined an inertial coordinate system you can use these laws to predict the motions of particles. (I'm not going to write the laws down here, but you can find them in many standard textbooks.) The second difference between the two systems, however, is that the transformation between inertial coordinate systems is also more complicated in SR than it is in Newtonian mechanics. I explain this idea in more detail in what follows.
Remember that once you have specified the laws of physics in any coordinate system you know them in all others, because you can always transform from one to the other. Suppose, then, that we try to repeat the calculation we discussed in the previous section. We start with an inertial system, where we know the laws of physics, and we define a new system such that at each point x'=x, y'=y, t'=t, and z'=t+4t. This time we will find that the new system is not inertial. The laws of physics in this new coordinate system are different, and more complicated, than the laws were in our inertial coordinates. For example we will find that in these new coordinates particles do sometimes have a coordinate speed dz/dt that is greater than the speed of light. If we play around enough, however, we will find that there is a particular set of transformations you can apply to an inertial coordinate system, known as a Lorentz transformation, that will generate a new coordinate system where the laws of physics have their usual, special relativistic form.
What if I want to formulate physics in some other coordinate system, e.g. one that is rotating or linearly accelerating relative to the first one? In Newtonian mechanics, the result was fairly simple. Newton's second law remained unchanged except for the addition of some new terms to the left-hand-side. In SR the result is far more complicated and I won't attempt to describe the mathematics of it here in any detail. For now I will simply note that such a description must be possible since you can always transform coordinates from an inertial system to make predictions in any other coordinates. The mathematics of GR is precisely the mathematics needed to describe a relativistic world in an arbitrary coordinate system.
What this tells us is that the laws of GR must be formulated in a very different way from the laws of Newtonian mechanics or SR. In both of those theories we wrote down laws for how the coordinates of a particle would behave. Newton's first law, for example, says that for a free particle d2x/dt2= d2y/dt2= d2z/dt2=0. These laws are then taken to be true for a certain class of coordinate systems, i.e. inertial ones, and physics in any other coordinate system is then derived from that. The statement that there are no inertial coordinate systems in the presence of gravity means you can not write down a set of laws for the behavior of the coordinates in any particular, special set of coordinate systems. Instead the laws of GR are written down in a coordinate-independent way. They still tell you how to calculate coordinate-dependent quantities like x(t), but they do so in a way that is equally valid for any coordinate system.
To do calculations, one must still specify some set of coordinates. If there is no gravity then this coordinate system may or may not be inertial; if it is the laws reduce to those of SR. If there is gravity the coordinate system definitely will not be inertial. Whatever the case may be, you then have to characterize what spacetime is like in this coordinate system. Given that characterization, GR can then tell you how to write down the laws of physics in a way appropriate for that particular coordinate system. The next section thus describes the main tool used in GR for characterizing a spacetime. It's called a metric.
ds2=dx2+dy2.
The metric itself represents this information in the form of a tensor. Roughly speaking you can just think of that as a matrix, although mathematically it must satisfy certain conditions. The rows and columns of that matrix represent the different coordinates, x and y in this example, and the elements of the matrix tell you the coefficients of these coordinates in the distance formula. For example, if I call my metric g (which is the usual convention) then g11 and g12 in this example would be the coefficients of dx2 and dxdy respectively. In this case they are one and zero. The entire metric for this case is
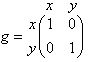
(Normally when metrics are written out in matrix form you won't see the labels for the rows and columns, x and y in this case, but I've included them here for clarity.) If you switch to polar coordinates the distance will now be expressed as
ds2=dr2+r2df2.
The metric for this coordinate system is
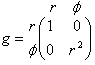
This is the same metric as the one described above for x and y. By that I mean that if you pick any two points in this space either distance formula will give you the same answer. If you write down two metrics such that you can find a coordinate transformation that goes from one to the other, then they are simply different ways of describing the same space (or spacetime). You can get a feeling for how this works by working out the metric for a more complicated coordinate system. For example, if you define x'=x2+y2, y'=y, you can show that the metric in these new coordinates looks like

A quick note about notation: Technically speaking, the matrix g is the metric. Nonetheless, it clearly contains the exact same information as the distance formula, just written in a different form. For that reason physicists often say they are writing the metric when they write the formula for ds2. I will unapologetically follow this practice below.
ds2=dx2+dy2+dz2-c2dt2.
(Some authors make the spatial components negative and the time component positive. This is purely a matter of convention and makes no physical difference.)
On the face of it this is a pretty strange looking metric. Spatial distances are just what we're used to for Cartesian coordinates, but according to this metric the squared distance between two events occurring at the same place but different times is actually negative. Mathematically this means that ds isn't really a distance at all; it's simply a convenient quantity that shares some of the properties of a distance function. In practice ds2 is more useful to work with than ds itself. It's often called the spacetime interval. (Some authors call ds the spacetime interval for consistency with the usual definition of distance.)
One important thing to note about this interval is that for any two events you can characterize the separation between them by whether the interval is positive, negative, or zero. It can only be zero between two events if their spatial distance is equal to the time between them times the speed of light. In other words a light beam emitted at one event will exactly reach the other one. Such events are said to have a lightlike separation. If the interval is positive then the separation is spacelike and if it's negative then the separation is timelike. If you think back to our discussion of light cones in the previous paper you can see now that you can summarize the causal structure of spacetime by saying that one event can cause another only if the separation between the two is timelike or lightlike. That's exactly equivalent to saying one event lies on or inside the future light cone of the other.
What makes such a description useful is the fact that it is valid in different coordinate systems. I claimed that the metric I wrote down above is the metric for SR. That claim could only make sense if the metric were the same for any inertial coordinate system. In fact you can check that if you perform a Lorentz transformation on the coordinates x and t the metric in terms of the new coordinates will be the same, i.e.
ds2=dx'2+dy2+dz2-c2dt'2. (You can find the Lorentz transformations written down in many standard texts or on the Web. Try checking that they leave this form of the metric unchanged.)
In GR we still talk about the spacetime interval. What makes this quantity so useful is that for any two points the interval is the same in any coordinate system. In other words if you do a transformation from one coordinate system to another you recalculate the metric components in such a way that the interval between any two points remains the same. We saw a concrete example of this above when we switched from Cartesian to polar coordinates. The components of the metric looked different in the new coordinates, but the result was the same.
At the risk of being redundant, I can now restate the relationship between SR and GR in yet another way. In GR you describe any spacetime in any coordinate system by specifying the components of the metric. The laws of physics applicable in that coordinate system are then given in terms of those metric components. If you change coordinates you get new metric components and the resulting equations look different, but all physically measurable results must come out the same. If and only if there is no gravity acting, you will be able to find a coordinate transformation that puts your metric in the form
ds2=dx2+dy2+dz2-c2dt2.
If you express the laws of GR for this particular metric, they will be exactly the laws of SR. In cases where there is gravity, of which we'll see an example below, no coordinate transformation will get the metric into this form.
Recall from the previous paper that we defined a geodesic as the path of shortest distance between two points. Technically the definition is more complicated, but in practice you can still think of it as the path that minimizes the spacetime interval between two points. It is still true, for example, that a timelike geodesic connecting two events will be the "shortest" timelike path between those two events, meaning the one with the smallest spacetime interval.
In an inertial coordinate system the geodesics are simply straight lines. For most coordinate systems the geodesics will be more complicated, but it should be intuitive that the metric gives you all the information you need to find the geodesics in your space. The metric tells you the interval ds2 between any two nearby points, and by integrating that quantity along any path you can find the total interval along that path. You can then find a formula for the path with minimal interval. To do this in arbitrary coordinates is somewhat tricky in practice, but the problem has been solved and there are formulas worked out for how to write down the geodesics in any coordinate system provided you know the metric.
The law of inertia, Newton's first law, can now be generalized to say that in any spacetime, described in any coordinate system, free particles will move along geodesics. Recall our discussion of this law in the previous paper, where I noted that in flat spacetime the geodesics are lines of constant velocity. Strictly speaking that statement is only meaningful in an inertial coordinate system. If I use spherical coordinates or accelerating coordinates or some strangely warped coordinate system I will not in general find that dx/dt remains constant along geodesics. Nonetheless if the spacetime is flat I can always find a coordinate transformation to a set of coordinates where all free particles move along paths with dx/dt, dy/dt, and dz/dt all constant.
If there is gravity acting in my spacetime then I will be unable to do so. If I somehow assign coordinates to all points in spacetime and measure the paths of free particles I will not find all those derivatives constant, and no coordinate transformation I can think of will be able to make them so.
Once again I want to emphasize that physical results do not depend on your choice of coordinates. If I look at the equations for geodesics, i.e. paths of free particles, they will look completely different in different coordinate systems. Nonetheless any given geodesic will still be comprised of the same set of points in spacetime no matter what coordinate system I use. The choice of coordinates is just a choice of how to label those points.
The law of inertial is a clear example of what it means to say that the laws of GR are coordinate-independent. To apply this law and make calculations you always need to specify a particular coordinate system. Nonetheless the law itself can be stated in a general way that is equally valid for all coordinate systems.
I can write the Einstein equation in a very concise form:
Gij=8p(G/c4)Tij
Unpacking what this equation means is a little more complicated, however. Recall that the metric is a tensor, an object that is represented by a 4x4 matrix. (It's 4x4 because there are four spacetime coordinates.) There is a set of rules that tells you how to form a new 4x4 matrix out of different time and space derivatives of the metric components. This new tensor is called the Einstein tensor, and is represented in the equation as Gij. (Tensors are often written with subscripts like this, which indicates their components. For example G00 is the upper left entry in the matrix for the Einstein tensor.) On the matter side of the equation Tij is a tensor called the energy-momentum tensor, made out of different properties of the matter and energy in your space (density, pressure, various shears, etc.). If you know all about the matter filling your space, the Einstein equation tells you how the metric components will evolve.
Note that this is a tensor equation, meaning it sets each of the components of the Einstein tensor proportional to the corresponding component of the energy-momentum tensor, so in reality there are 16 Einstein equations. In practice they are never all independent, and for spacetimes with a high degree of symmetry such as cylindrical or spherical symmetry, there are often only a few independent components of the Einstein equation.
Just as GR's law of inertia reduces to the Newtonian one in the limit of a flat spacetime, so too the Einstein equation has a Newtonian parallel. In regions where gravity is very weak, meaning the spacetime is nearly flat, and all objects are moving much slower than the speed of light, the Einstein equation can be shown to reduce to Newton's law of gravitation. What this means is the following: Say you have two light objects far away from each other and moving slowly. You can use the Einstein equation to find the metric for this spacetime. The metric components will be different for different coordinate systems, but you can define a coordinate system in which the metric looks like the SR metric (i.e. flat) plus small corrections. If we assume these objects experience no non-gravitational forces, then we can calculate their motion simply by finding the geodesics in this spacetime. Doing so we will find that they accelerate towards each other at a rate given by
![]() ,
,
where m is, for each object, the mass of the other one. This is precisely Newton's law of gravitation. Thus GR automatically reproduces all the successful predictions of Newtonian gravity. For situations where relativistic corrections become important—strong gravitational fields and/or speeds near the speed of light—the predictions of GR differ from those of Newtonian gravity. In every case that has been tested the predictions of GR have been shown to be correct.
Now, at long last, I can now move beyond all of these abstractions and give an example to illustrate how these ideas can be put into practice.
If we want to write a metric for such a spacetime there are very few possibilities. We should treat x, y, and z on an even footing to ensure isotropy, and none of the metric components should depend on space to preserve homogeneity. Neglecting cross-terms such as dxdy, the most general way to write such a metric is
ds2=a2(t) (dx2+dy2+dz2) - b2(t)c2 dt2.
In fact this formula can be simplified further without any loss of generality by redefining a new time coordinate
tnew = b(t) t,
which eliminates b(t) in the metric. Just to simplify the equations I'll use t from now on to mean the new time I just defined, so the metric can now be written as
ds2=a2(t) (dx2+dy2+dz2) - c2 dt2.
This metric is known as the flat Friedmann-Robertson-Walker metric. Technically this metric is not the most general possibility for a homogeneous, isotropic spacetime. If I had included cross-terms in the original metric it would have opened up a couple more possibilities, but for simplicity I'll just talk about this one.
Note that I could always write this metric in a more complicated way that wouldn't look homogeneous or isotropic by choosing different coordinates. However, the statement that my spacetime is homogeneous and isotropic is equivalent to the statement that it is possible to find a set of coordinates such that the metric is independent of space and symmetric in all the spatial coordinates. Compare this fact with the one we saw earlier that saying a spacetime has no gravity acting in it is equivalent to saying you can find an inertial set of coordinates. The properties of spacetime are the same no matter what coordinate system you use to describe it. The physical properties of the spacetime, however, limit the possible ways you can write the metric.
The previous paragraph is a bit dense, but it contains one of the most important ideas of this paper. I urge you to consider it carefully before moving on.
Returning to the flat FRW metric, note that no possible coordinate transformation will change the form of this metric into the SR metric. Suppose for example that we tried to do this by defining new coordinates x'=a(t) x (and likewise for y and z). That would set the coefficients of dx2, dy2, and dz2 to one, but it would also introduce new cross-terms such as dxdt. You can try playing around with this for a while and I think you should be able to convince yourself that unless a(t) is a constant you can not reduce this metric to an inertial one.
The nature of the spacetime described by this metric depends on the behavior of the function a(t), which at any given moment could be increasing, decreasing, or constant. For now let's focus on the first case, where a is increasing with time. In that case this metric describes an expanding universe. We know that because the metric tells us how to compute distances between points, so if a is increasing with time then the distance between two points x1 and x2 is getting larger.
To go further we could use Einstein's equation, which relates the metric components to the matter and energy in the spacetime. If you make certain assumptions about the matter filling space (for the experts, you assume it's a perfect fluid), the equation becomes particularly simple. Since this example is so highly symmetric, there are only two independent Einstein equations:

where dots indicate time derivatives and r and p are the energy density and pressure of the matter respectively. The most important thing to note about these equations comes from the first one. Assuming there is any matter in the universe, a(t) can not be constant. In other words a flat FRW universe must either be expanding or contracting. The prediction that the universe can not be static was one of the most startling early results of GR. For a discussion of the implications of this result see my paper The Expanding Universe.
We could continue discussing the properties of this spacetime. Given this metric, for example, you could find the geodesics to see how free particles would move, or you could find the light cones, which tell you about the causal structure of the spacetime. My purpose with this example, however, was simply to illustrate the basic idea of how you can use a metric to describe a given physical situation. Another example, which I won't discuss in any detail, is the spacetime around a spherical object like a star. By assuming the spacetime is spherically symmetric and static you can narrowly define the space of possible metrics, much like we did here. Similarly, you can study more complicated situations like spinning stars (which are no longer spherically symmetric) or collapsing stars (which are no longer static). For each of these cases, you can write down a form of the metric valid in some coordinate system. Once you know the metric, you know everything there is to know about the spacetime.
In GR you still have matter and you can describe it in much the same way as before. In addition, however, the spacetime itself is now dynamic and requires characterization. You achieve this by specifying the metric, which is to say the formula for the interval between any two points in spacetime. The component description of the metric will be different in different coordinate systems, but always in such a way that the interval between two spacetime points is the same regardless of the coordinate system being used. The laws of GR then tell you both how the matter will evolve in this metric and how the metric will behave in response to the matter inside it. Assuming no non-gravitational forces are acting, these equations will be sufficient to determine the future evolution of the system from any initial starting point. (If there are other forces then you have to use the appropriate force laws as well, just as you did in Newtonian physics.) This procedure works equally well in any coordinate system. In a spacetime with negligible gravity, however, you can find a coordinate system where the metric, and thus the laws of physics, reduce to the relatively simple forms they have in SR.
As a last point, I want to mention one law of SR that continues to hold true even in the presence of gravity. No matter what the spacetime is like, GR still says that the speed of light is an absolute limit. Particles always move along timelike or lightlike curves, so any two events outside each other's light cones can not be causally connected. (If you're dealing with fluids instead of particles then you say that wave fronts move along timelike or lightlike paths. The basic conclusion, namely that spacelike separated events can not influence each other, remains valid.) Note that you can always choose coordinates where the coordinate speeds, e.g. dx/dt, are greater than c. However fast you may be moving in those coordinates, however, a light beam shining ahead of you will be moving even faster. Put in simple physical terms, you can't outrace light.
GR is often called a geometrical theory of gravity. Rather than viewing gravity as a force GR describes it as an interaction between matter/energy and the geometry of spacetime. Meanwhile, the other forces like electromagnetism are still viewed in essentially the same way as before. They now act in the geometry defined by gravity, but otherwise they are still treated as pushes and pulls that particles exert on each other. Many people, including Einstein, have found the geometrical description of gravity so compelling that they have tried to come up with similar descriptions of the other forces as well. Thus far all such attempts have failed. Nonetheless, with the advent of GR, geometry has entered physics as a dynamical quantity, and we now know spacetime to be a much richer place than Newton could have dreamed.
 Gary and Kenny Felder's Math and Physics Help Home Page
Gary and Kenny Felder's Math and Physics Help Home Page
www.felderbooks.com/papers
 Send comments or questions to the author
Send comments or questions to the author