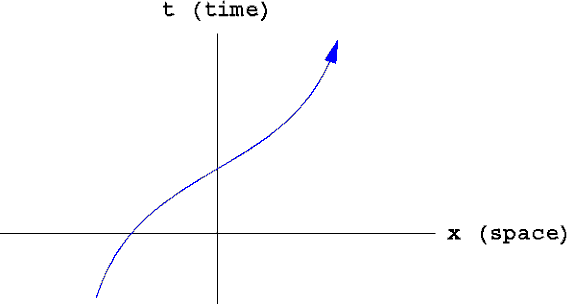
The world line of an object in a one-dimensional space
For readers with a stronger background in physics there is also a sequel paper which goes into somewhat more detail about how the laws of general relativity are formulated. That paper assumes a working knowledge of calculus and introductory physics such as you would get in the first year or so of a university physics major.
1) General relativity is a theory of the behavior of space and time
Prior to the 20th century all physics theories assumed space and time to be absolutes. Together they formed a background within which matter moved. The role of a physical theory was to describe how different kinds of matter would interact with each other and, by doing so, predict their motions. With the development of special and later general relativity theory in the early 20th century, the role of space and time in our theories of physics changed dramatically. Instead of being a passive background, space and time came to be viewed as dynamic actors in physics, capable of being changed by the matter within them and in turn changing the way that matter behaves.
In GR, spacetime becomes curved in response to the effects of matter. I will discuss below what it means for spacetime to be curved, but just to give a flavor of this idea I can note here that in a curved spacetime the laws of Euclidean geometry no longer hold: the angles of a triangle do not in general add up to 180°, the ratio of the circumference of a circle to its diameter is in general not p, and so on. This curvature in turn affects the behavior of matter. In Newtonian physics a particle with nothing pushing or pulling it (no forces acting on it) will move in a straight line. In a curved spacetime what used to be straight lines are now twisted and bent, and particles with no forces acting on them are seen to move along curved paths.
2) General relativity is a theory of gravity
Newtonian theory, which held sway prior to the 20th century, described gravity as a force. In other words two massive bodies like the Earth and an apple were understood to exert a pull on each other as a result of the law of gravity. If an apple started out at rest, say just as it broke off from a tree, then gravity would cause it to move towards the Earth until it collided with it. Newton's law of gravity was able to explain in detail not only the fall of apples, but also the orbit of the moon about the Earth, the motions of the planets about the sun, and much more. GR can also explain all of those things, but in a very different way. In GR, a massive body like the sun causes the spacetime around it to curve, and this curvature in turn affects the motion of the planets, causing them to orbit around the sun.
In later sections I'll discuss in more detail how GR describes results like falling apples and orbiting planets. For the most part the predictions of GR and Newtonian gravity are very similar. There are small differences that can and have been measured in the solar system, however, and to date all the data have matched the predictions of GR. Moreover, there are certain situations, like the vicinity of a black hole, where GR makes predictions drastically different from those of Newtonian theory. I will briefly discuss some of these later and talk about what evidence we have for some of the more exotic predictions of GR.
In short, GR is a theory in which gravity is described by saying that space and time are dynamics quantities that can curve in response to the effects of matter and can in turn alter the behavior of matter. Before I discuss GR in any greater depth, I need to talk more generally about the idea of curved spaces. The next section thus discusses what it means for space to be curved. In GR, however, it is not just space but spacetime that is curved, and the following section discusses that idea. Using these ideas I then describe how gravity is viewed in GR. Having thus presented the basic ideas of GR, I go on to discuss a number of applications where GR gives results very different from those of Newtonian theory. In the conclusion I discuss some of the open questions remaining in our understanding of the nature of space and time.
For the sake of completeness, I can note here one other way of describing the content of GR, which is that GR is a theory of physics in arbitrary coordinate systems. The laws of physics that were known prior to GR, most notably Newtonian physics and special relativity, were only valid in a restricted set of coordinate systems known as inertial reference frames. The laws of GR are formulated in a way that is equally valid in any reference frame. In my sequel paper I explore this idea in greater depth.
To test this idea you would need a definition of exactly what a straight line is. We know that one of the properties of straight lines is that if they are parallel then they stay parallel, so clearly the paths you and your friends walked on can not be straight lines. On the other hand we also know that a straight line is the shortest distance between two points. So if you were accidentally walking on a curved path then you should be able to draw a path connecting your initial and final points that is shorter than the one you actually walked along. To picture this test you can imagine that you were laying down a trail of red paint behind you as you walked. You can carefully measure your red trail with a tape measure. Then you can try to paint a shorter, blue trail connecting your initial and starting points. If your path was curved, you should be able to make a shorter path.
If you are living in a curved space, however, then you might fail. In other words it is possible that you and your friend each took the shortest possible route between your starting and ending points, and yet you ended up slowly turning away from each other. In a curved space paths that stay parallel to each other are not the paths of minimal distance and vice-versa. Since there is no path in such a space that fits all our usual notions of a straight line, mathematicians came up with another word to use for this situation. In any space, the shortest path between two points is called a geodesic.1 In a flat space, meaning one with no curvature, the geodesics are normal straight lines that stay at a constant angle to each other. In curved spaces they are generally more complicated.
You may at this point be having trouble picturing exactly what is happening. If you picture two paths that start out parallel to each other and end up pointing away from each other then it seems that they must be bending, and they couldn't possibly be geodesics. This problem stems from the fact that our brains are designed to think in terms of flat geometry, so we can not picture a curved space any more than we can picture a four dimensional space. Fortunately there is a trick we can use to imagine more clearly how this works.
Imagine very small ants walking on the surface of a globe. Two ants start out at different points on the equator heading due south. The paths they are walking along are initially exactly parallel. If neither ant turns then they will continue heading south until they reach the South Pole. In other words they can start out moving on parallel paths, walk straight the whole way, and yet end up at the same point. On the surface of a sphere, the geodesics do not stay parallel to each other. Such a space, where parallel lines tend to curve inwards towards each other, is said to have positive curvature. To picture a negative curvature space, where parallel lines curve outwards, you could put the two ants on the surface of a saddle. The sign of the curvature is determined by whether parallel lines bend towards or away from each other, and the magnitude of it (how big a number it is) is determined by how quickly they do so. A space with large, positive curvature, for example, is like the surface of a very small sphere.
We've just used a trick called embedding, which means describing the properties of a curved space by considering it to be a curved surface in some higher dimensional flat space. This trick is very useful because it allows us to use our natural ability to picture flat spaces when trying to understand curved spaces. There is a danger, however, of taking the embedding too literally. If you picture a geodesic on the surface of a sphere you might be inclined to think that it's only a sort of fake geodesic. If I really want to find the shortest path between the equator and the pole I can make a straight line that goes through the interior of the sphere. I only called the ant's path a geodesic because I had put on the limitation that it wasn't allowed to move off the surface. That's true for the embedded space, but it's not true for a real curved space. A particular two dimensional curved space might have the same mathematical properties as the surface of a sphere, but that doesn't mean that it actually has to exist in some flat, three dimensional space. In fact not all curved spaces can be embedded in this way. So I would urge you to use embedding as a tool for picturing the properties of curved spaces, but always remember that it is just a tool. In general curvature is simply an intrinsic property of a space.
To wrap up this section, I want to note one more property of geodesics, which is that to an observer in the curved space they will appear straight on short enough scales. Imagine that instead of an ant on a globe our traveler is once again you, now moving on the surface of the Earth. Let's assume for simplicity that the Earth is a perfect sphere with no mountains or canyons. If you can only see a few miles in any direction then the surface of the Earth appears flat; you would need to see much farther than that to notice the curvature. In this seemingly flat space you can draw geodesics and they will look to you like straight lines. If you started laying out one foot rulers end to end you could circle the whole Earth and at each point it would seem to you that you were marking out a straight line, yet if you marked out two such lines that started parallel you would eventually find them converging.

Spacetime diagrams such as the one above are critical to relativity, so I would urge you to spend a little time playing with them in your mind now to get comfortable with them. For instance, try to answer the following questions before you read on. (I give the answers in the next paragraph.) What's the world line of a particle at rest? What's the world line of a particle moving with constant speed in one direction? How would you describe the motion of a particle with the world line shown below?
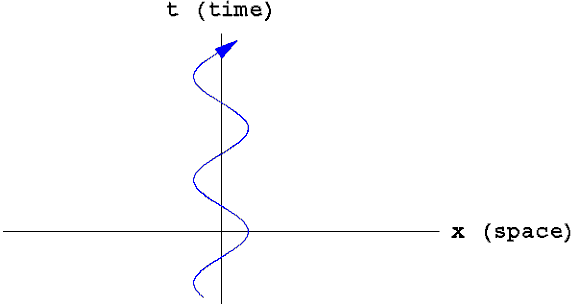
The answers: The world line of a particle at rest is a vertical line. As time (t) moves forward it always stays at the same position (x). The world line of a particle moving at constant velocity is a tilted line. In each interval of time, say each second, the position of the particle changes by some constant amount. Finally, the world line shown above describes a particle that's oscillating, like a mass on a spring. As time progresses the particle moves back and forth periodically. Once again, I would urge you to make sure you are comfortable with these ideas before reading on.
Viewing space and time this way allows us to formulate physics in a new way. Consider, for example, Newton's first law, which states that an object with no forces acting on it will move in a straight line at a constant speed. Another way to say this is that the world line of a free object (one with no forces on it) is a straight line.
Be careful not to confuse an object's motion in space (its trajectory) with its motion in spacetime (its world line). The latter contains more information than the former. For example, saying that the world line of an object is a straight line tells you not only that its trajectory is a straight line, but also that it is moving with constant speed. As another exercise, try to picture the world line of a particle accelerating in a straight line. Try to picture the world line of a particle moving in a circle at constant speed. (This last exercise requires two spatial dimensions, and hence a 3D spacetime.)
In Newtonian mechanics the notion of spacetime is unnecessary. You are free to think of space and time as separate things and formulate Newton's laws in terms of the motion of particles or think of them as unified and formulate those laws in terms of world lines. In fact the former description is simpler and easier to work with. In relativity, however, (both special and general) it is necessary to view spacetime in a unified way. In GR this unified spacetime is curved by the effects of gravity. Newton's first law continues to hold in GR, but in a generalized form: A free particle will move along a geodesic. In the presence of gravity, however, that geodesic will in general be more complicated than a simple straight line.
In a Newtonian picture these objects will exert a mutual gravitational attraction, causing them to accelerate towards each other until they eventually collide. In GR the same effect will occur, but the description will be very different. Because gravity is not a force in GR, and we said the objects neither exert nor feel any non-gravitational forces, the objects should act like free particles, moving along geodesics. (Such an object experiencing no non-gravitational forces is said to be in "free fall," like an object falling towards the Earth with no other forces on it.) In a flat spacetime—no gravity—the geodesics would be straight lines. In particular, since we specified that the objects started out at rest, their world lines would be vertical lines. In other words they would always stay the same distance from each other.
When we consider the effects of gravity, however, we know that the objects will warp the spacetime around them. Recall that in a curved space, parallel lines do not always stay parallel. In this particular curved spacetime, the geodesics followed by the objects start out parallel but converge over time. Thus the objects eventually collide. Qualitatively the result is the same as predicted by Newton's theory, but the underlying description is radically different.
To show how this works more explicitly, I'm going to assume for simplicity that one body is much heavier than the other. For example this could be a description of the sun and the Earth. That way we can ignore the gravitational effects of the smaller body and just consider what spacetime looks like around a single, massive object. The spacetime diagram for this situation is shown below with a couple of geodesics drawn in.
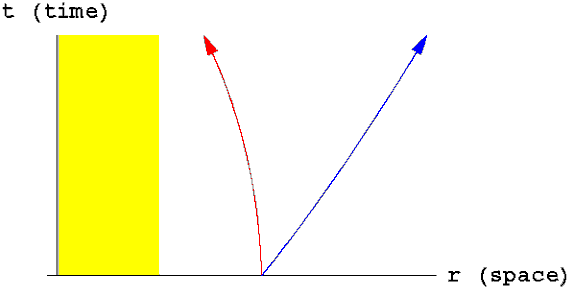
The yellow rectangle in this diagram is the sun itself. Of course the space around the sun is really three-dimensional, but the spatial dimension in this diagram is just a line going directly outward from the sun. I've labeled the spatial axis "r" (for radius) rather than "x" to remind you that I'm only showing one of the three spatial directions. This means the geodesics I've shown are for particles moving directly towards or away from the sun. The full spacetime diagram would also have geodesics corresponding to stable orbits around the sun like those of the planets. (Try to picture what those would look like.) Bearing in mind that only one spatial direction is shown, think about why the sun should appear as a rectangle in the diagram.
The red geodesic shows that an object initially at rest will curve in towards the sun. Even an object initially moving away from the sun could fall back in if it were moving slowly enough. The blue geodesic, however, is for a particle starting out at the same place but with an initial outward velocity large enough that it will never fall back. Such an object is said to have escape velocity.
This description is all very interesting, but so what? If the measurable results are the same as they were in Newtonian theory, why invent this new, more complicated theory? The answer is that the measurable results are not the same. Qualitatively the behavior described above is the same in both theories, but the exact details come out slightly different. In particular, you can prove that when you have weak gravitational fields and objects moving much slower than light, the predictions of GR are very close to those of Newtonian theory. That had to be true for GR to be a viable theory because we know that to high accuracy Newtonian theory had worked to predict the effects of gravity in many situations. When you violate those conditions, however, the predicted results begin to diverge.
Without giving you the math behind GR I can't describe in any detail why or how these predictions diverge, but I can give you some examples of the new predictions of the theory. For instance, I said above that Newton's theory of gravity accounted for the orbits of the planets. Strictly speaking, however, there was a tiny discrepancy between theory and observation in the orbit of Mercury, the planet closest to the sun (where the sun's gravity is strongest). Mercury is observed to precess, meaning the long axis of its ellipse revolves slowly around the sun, at a rate greater than predicted by Newton's theory. Specifically, the axis revolves faster than the Newtonian prediction by one degree every 8300 years! GR predicts this precession exactly.
More interesting than such numerical predictions, however, are some of the qualitatively new effects that can occur in GR. In the next section I describe a few of them.
(From this point on I will omit units when writing distances and times. All times will be in years and all distances will be in light-years. In these units the speed of light, c, is equal to one.)
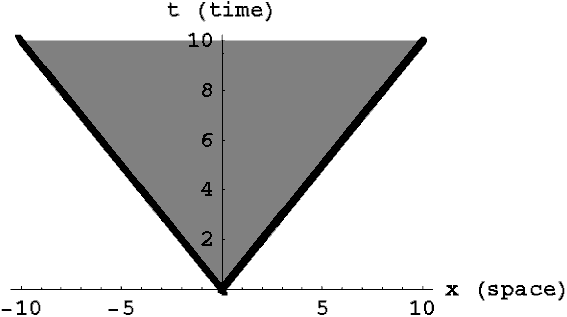
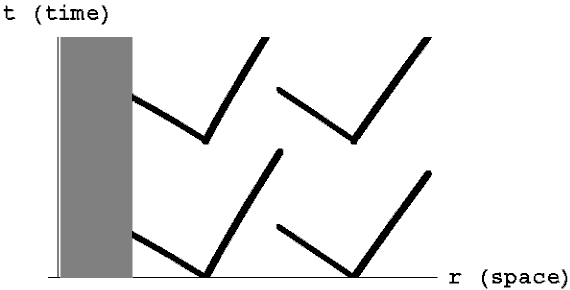
To see this another way, consider the spacetime diagram above for a spacetime with no gravity. Mathematically this is the limit where general relativity reduces to special relativity. The bold lines represent the paths light beams would follow if I emitted them at the origin (x=0, t=0) either to the right or left. The shaded region in between these two lines represents all the points in spacetime that I could send a signal to. These points are said to be inside my (future) light cone. For example the point (x=7 light years, t=4 years) is outside the light cone. Nothing that I do at (x=0, t=0) can possibly have an effect on what happens at (x=7, t=4) or vice-versa. Note that this light cone is particular to a specific point in space and time, namely (x=0, t=0). If I were to draw the light beams emanating from this same point in space (x=0) at a different time, for example, they would demarcate a different region of spacetime.

In addition to the future light cone, there is also a past light cone associated with each point in spacetime. In the diagram above the bold lines at negative times represent light beams that would reach me at (x=0, t=0) coming from either direction. You should take a moment to convince yourself that the region in between those two lines represents all the points in spacetime that can have affected me. For example my friend at x=7 can send a signal to me at t=-9 telling me what to do at time t=0, but if she sends the signal at t=-3 it will be too late for that signal to reach me by t=0.
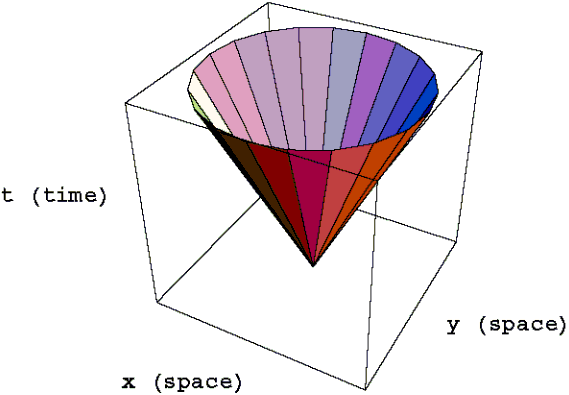
Finally, for those of you wondering what any of this has to do with cones, the diagram above shows a spacetime diagram with two spatial dimensions instead of one. The figure in this diagram represents the paths of light beams moving in all possible directions. This figure is the aptly named "light cone" for the point (x=0, y=0, t=0).

Light, like everything else, is bent towards the object. This means that the light cones are now somewhat bent, but the bending is very slight. Recall that the future light cone shows the limits of the possible world lines of particles. Particles moving away from the sun can not outrace the outgoing light beams. Since these are bent slightly towards the sun in the spacetime diagram, a signal sent outward to my friend three light-minutes away from me will take longer than three minutes to reach her. Conversely a signal sent to my other friend who is floating three light-minutes closer to the sun than I am could take less than three minutes to reach him. This doesn't violate the rule that nothing can move faster than light because the signal must still lag behind (or exactly match) a light beam moving towards the sun.
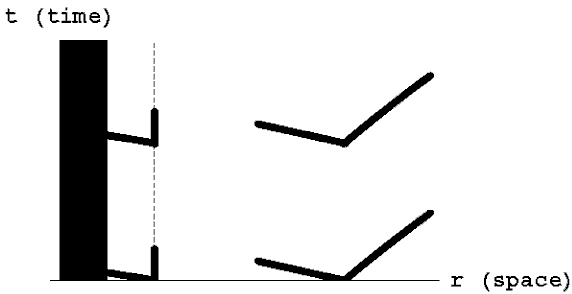
What happens if we consider something denser than the sun? For example a neutron star is an object a few times more massive than the sun but only about ten miles across. Very close to the surface of such an object the gravitational field is very strong, and geodesics are all very strongly bent, as shown in the diagram below.
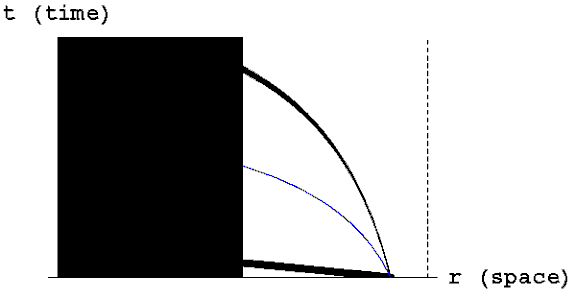
What happens when an object becomes even denser than a neutron star? Consider a hypothetical object with the mass of the sun but a radius of only half a mile. I show below the spacetime diagram for such an object.
The light cones very near the object are so strongly bent that a light beam shined directly outwards can not escape from the gravitational field of the object. Recall from above that the light cone emanating from a particular point in spacetime defines the region to which one can send a signal. If you are sitting close enough to the object shown above, then any light beam, carrier pigeon, or rocket ship you try to send out—including yourself—can only move closer to the center of the object.
An object so dense that it acts like this is called a black hole because even light can not escape from it. The place where the light cones start to turn inwards is called the event horizon. I've indicated it with a dashed line in the diagram above. That's the point of no return; if you cross inside the event horizon you can never get back out again. Remember that I'm only showing radial distance in these diagrams, so the event horizon looks like a point in space, and thus a line in spacetime. In the full three-dimensional space the event horizon is not just a point but rather a sphere surrounding the black hole.
On the event horizon, the outer edge of the light cone is vertical. Recall that the two branches of the light cone represent the paths taken by light emitted in either direction. That means that if you were exactly at the event horizon and shined a beam of light directly outward the light would eternally hover at this same radius. If you were inside the event horizon, the outer edge of the light cone would actually be tipped inwards. In other words whether you shined light inward or outward it would still approach the center of the black hole. The motion of any object, such as yourself, is bounded by the light cone. Thus if you are inside the event horizon you must approach the center.
What would that look like to you? If you shined a light beam away from the black hole would you see it turn around and start rushing towards the center? No. The light would be approaching the center, but you would be approaching it even faster. From your point of view the outgoing light beam would be moving away from you at exactly the speed of light. This is a general property of GR. No matter how strange a given spacetime might be, a local observer will always see light beams moving in all directions at exactly the same speed. This is the sense in which GR preserves the special relativity rule that says nothing can move faster than light. Your coordinate speed might be faster than c, but you will never see yourself catch up to a light beam.2
One could easily write an entire paper about the strange behavior of black holes, but here I will simply note a few of their more important properties. First, consider the massive object in the center. That object is the source of the gravitational field, but each particle in the object is itself living in the spacetime we've been describing. That means that it can not stay at rest but must move towards the center. In other words once an object has become dense enough to form a black hole it must keep collapsing and getting denser. If gravity were a force you might imagine some repulsive force strong enough to overcome it even in these extreme circumstances. As it is, however, no conceivable force in the universe could possibly resist this pull because spacetime itself is so strongly bent that there are no paths leading out.
In fact you can calculate the maximum time that a particle could possibly take to fall in to the center of the black hole, assuming it was being pushed outwards with an arbitrarily strong force, and the result is finite. Thus the object that formed the black hole originally will keep collapsing down and within a finite time it will have all collapsed into a single point in the center. Such a point of infinite density is called a singularity.3
To sum up, massive, dense objects exert strong gravitational fields, warping the spacetime around them. For an object of any given mass, there is a characteristic radius called the Schwarzschild radius with the property that if the object gets squeezed into a sphere of that radius or smaller it will become a black hole. If that happens it will continue to shrink until a short time later it forms a singularity. The Schwarzschild radius for an object of mass m is 2G m/c2, where G is Newton's gravitational constant. For example the Earth, in order to become a black hole, would have to be squeezed into a sphere less than 5 mm across.
The event horizon of a black hole is a sphere at the Schwarzschild radius. Note that as the object inside the black hole collapses its mass remains constant, so the size of the event horizon remains fixed at the Schwarzschild radius 2G m/c2. That means that if we were to observe the formation of a black hole we would see an object (typically a dying star) collapse down to within its Schwarzschild radius and disappear. The theory tells us that the object would continue to collapse after that, but without going in ourselves to take a look we can never directly observe that fact. From the outside, once a black hole has formed you can't tell what's going on inside it. This property is usually referred to by the whimsical phrase: Black holes have no hair.
GR tells us that light rays (and everything else) get bent in the vicinity of a massive object. This means that a sufficiently massive object can act just like a lens, focusing the light from sources behind it. In fact this observation provided one of the earliest tests of GR. When the light from other stars passes near the sun it gets bent, which changes the apparent positions of the stars. (In effect the area of the sky behind the sun has been magnified to look bigger than it is.)

This effect is very hard to observe, first because the bending of the light rays is very small, but even more so because we can't normally see starlight close to the sun. We only see stars at night when we're looking away from the sun. The only exception to this is during a solar eclipse when the moon momentarily blocks the sun's light. Einstein first published the theory of GR in 1916. In 1919 there was a total solar eclipse and a team of scientists led by Arthur Eddington traveled to West Africa to observe the eclipse and check whether the starlight was deflected. The stars did appear to be slightly moved relative to their nighttime positions in exactly the way predicted by GR. This observation was the first crucial test of Einstein's theory.
This kind of magnification of a region of space is called weak gravitational lensing. If the object causing the lensing is massive enough, however, you can even bend the light so much that you see multiple images of another object behind it.
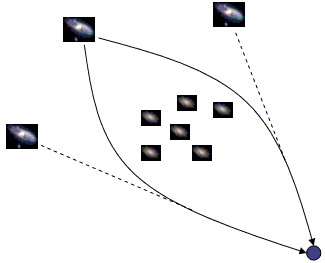
The production of multiple images in this way is called strong gravitational lensing, and has been observed dramatically in many instances by the Hubble Space Telescope among others.
In GR the same effect occurs for gravitational fields. Ripples in spacetime can induce other ripples in spacetime in such a way that you get a wave propagating through space. Thus if you take a heavy mass and shake it back and forth vigorously enough you will cause a spacetime ripple that will radiate outwards.
What would such a ripple look like? Say you were holding a spherical object as a gravity wave passed through where you were standing. The space around you would alternately stretch in two different directions, causing the sphere to get elongated first along one axis and then the other.

Such an effect could be detected in principle by measuring the time it takes a light beam to travel from one side of the sphere to another in different directions. In the presence of a gravity wave, the relative times in the two directions would oscillate.
In fact just such an experiment has been built recently. Instead of a sphere it uses two long perpendicular lines. These lines are actually evacuated chambers four kilometers long. Lasers are continually fired back and forth along both chambers. At the intersection of the two lines is a detector that can detect minute changes in the relative light travel times along the two paths. (For those familiar with optics the detector is actually a laser interferometer.) A regularly oscillating change would be the hallmark of a gravity wave. This experiment is called LIGO, or Laser Interferometer Gravitational Wave Observatory.

To date neither LIGO nor any other experiment has ever detected a gravity wave. The reason for that is simply that gravity is weak. Even in the vicinity of the sun the bending of spacetime by gravity is a small effect. Moreover to get a gravity wave it's not enough to have a massive object; something has to shake that object back and forth very vigorously. What could produce such violent behavior?
There are several candidate sources for gravity waves. The most dramatic, and potentially easiest to detect, are closely orbiting massive objects. Imagine for example two very dense objects like neutron stars or black holes orbiting around each other at a very small distance. From the point of view of a distant observer each of these massive objects would be swinging back and forth in the sky as they moved through their orbits. The result would be the emission of a strong gravity wave.
Gravity waves, like electromagnetic waves, carry energy. That means that the orbiting objects mentioned above would steadily lose energy as they emitted these waves. When an object in orbit loses energy it tends to fall inwards towards the center of its orbit. Thus the two objects would spiral in towards each other. This effect would be very gradual at first, but the closer they got the faster the oscillations would be. That means the rate of energy loss from gravity waves would increase, causing them to spiral in faster and faster until they collided. It is hoped that the last stages of an inspiraling pair of massive objects would produce gravity waves strong enough for us to detect on Earth.
Another possible source for gravity waves is the early universe. In the first few seconds after the big bang, the universe was an extremely hot, dense soup of elementary particles. At the very beginning, a tiny fraction of a second after the big bang, that soup would have been so dense that any ripples propagating through it could have moved enough matter around to emit strong gravity waves. If such waves could ever be detected they might give us direct observational data about processes occurring in the universe within its first fraction of a second of existence!
Shortly after Einstein developed the theory of GR, he and others thought of applying it to the question of cosmology, the study of the large scale structure of the universe. The equations of GR describe the nature of space and time, so in a sense it was natural to ask what those equations said about the nature of things on the largest scales. The answer is that the equations have no solutions that are static on large scales. More specifically, the equations of GR predict that the universe must either be expanding or contracting.
This behavior essentially comes from the attractive nature of gravity. If you were to have a universe where all the stars were at rest relative to each other, their mutual gravity would cause them to start moving towards each other. In Newtonian physics, it was assumed that the universe went on forever and thus the attraction felt by any given star would be equally balanced on all sides. In GR you can show, however, that even in such a case the space as a whole will contract and the distances between the stars will shrink.4 The universe could start out expanding, and depending on how fast it was expanding it might continue to do so or it might eventually stop and start contracting. It could never stay still, however.
A more complete description of what it means to say the universe is expanding or contracting would be beyond the scope of this paper. For a longer discussion of that issue see my paper on the Big Bang Model: The Expanding Universe. That paper also discusses the big bang itself and some of the evidence for the Big Bang Model in more detail than I do below. Here I simply note a few of the key ideas behind the model.
The conclusion that the universe couldn't be static seemed so implausible to Einstein that he attempted to modify the theory in order to allow static solutions. His modifications didn't work, however, and it remained an inescapable conclusion of the theory that the universe could not be static. In 1929, thirteen years after the publication of GR, Edwin Hubble observed that all distant galaxies appeared to be moving directly away from us in exactly the way predicted by GR for an expanding universe.
Nonetheless, while GR may be a beautiful theory, the ultimate judge of its value is not its aesthetic appeal but its ability to predict the results of experiments. Since the theory was first developed there have been a number of high precision tests of its predictions. I have already mentioned the precession of Mercury, the bending of starlight near the sun and galaxy images near large clusters, and the evidence for the expansion of the universe. Other pieces of evidence for the theory include a change in the speed of clocks near gravitational sources, the observation of objects believed to be black holes in the centers of galaxies (including our own), and more. Thus far in every case where an experiment or observation has been done to test a prediction of GR, the theory has been shown to be correct.
Meanwhile the early twentieth century saw another revolution in physics, the development of quantum mechanics. This theory completely changed our understanding of matter and energy. In quantum mechanics a particle is not seen as a simple dot existing at a particular place, but as a fuzzy wave existing as a collection of probabilities for where it could be and how it could be moving. A description of quantum mechanics would be beyond the scope of this paper, but for a general introduction see my paper with Kenny Felder on the topic: Quantum Mechanics: The Young Double-Slit Experiment.
Taken together these two theories—GR and quantum mechanics—form our best current understanding of the physical laws of the universe. The problem is that you can't take them together. Every attempt that has been made so far to reconcile the geometric view of spacetime in GR with the fuzziness of quantum mechanics has led to contradictions. The search for a single theory that could bring these two pieces together—a theory of quantum gravity—occupied Einstein for much of his life and is still one of the greatest outstanding challenges in science today.
There is currently one favored candidate called string theory, which essentially reworks quantum mechanics by treating particles as small strings rather than points. This simple idea has dramatic consequences for the theory, and it seems that it may be able to resolve the contradictions of quantum gravity. Unfortunately it's very difficult to do calculations in string theory, so the theory is still untested.
Regardless of whether or not string theory is correct, many questions certainly still remain. The nature of geometry on small scales where quantum mechanics is important is not understood. It's likely that some of our basic concepts of space, time, and causality may need to be radically changed on those scales. The history of the universe for the past fourteen billion years or so is pretty well understood, but what happened before that is not. Was there a big bang? What, if anything, happened before it? What will be the ultimate fate of the universe in the future?
In short, what Newton said about himself hundreds of years ago remains true of us today:
"I seem to have been only like a boy playing on the seashore, and diverting myself in now and then finding a smoother pebble or a prettier shell than ordinary, whilst the great ocean of truth lay all undiscovered before me."-Sir Isaac Newton
2Technically light beams inside matter don't move at the maximum speed c, so what I'm saying about light is only true in a vacuum. That fact is simply due to the nature of light and has nothing to do with the properties of spacetime. Whether you're inside matter or inside a vacuum the maximum speed is c, roughly 300 million meters per second.
3As we know from special relativity, the time it takes for a sequence of events to occur can be different from the point of view of different observers. When I say it takes a finite time for an object to reach the center of the black hole, I am talking about time as experienced by that object. In other words, if you fell into a black hole wearing an indestructible stopwatch, that stopwatch would still have some finite reading (depending on the size of the black hole) when you reached the center.
4It turns out that even in Newtonian physics a static universe would be unstable and the stars would eventually start collapsing in towards each other in different regions. This fact wasn't appreciated when the theory was developed, though.
 Gary and Kenny Felder's Math and Physics Help Home Page
Gary and Kenny Felder's Math and Physics Help Home Page
www.felderbooks.com/papers
 Send comments or questions to the author
Send comments or questions to the author