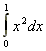 . None of this notation was particularly meaningful, but you sort of knew what it meant, and eventually life was comfortable.
. None of this notation was particularly meaningful, but you sort of knew what it meant, and eventually life was comfortable.
When you were first learning calculus, you learned how to calculate a derivative and how to calculate an integral. You also learned some notation for how to represent those things: f'(x) meant the derivative, and so did dy/dx, and the integral was represented by something like 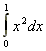 . None of this notation was particularly meaningful, but you sort of knew what it meant, and eventually life was comfortable.
. None of this notation was particularly meaningful, but you sort of knew what it meant, and eventually life was comfortable.
And then one day, your professor said something like "In this case, we divide dx by 2." Or worse, "let's multiply both sides of the equation by dx." It made as little sense as adding 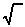 to both sides of an equation, or saying "we can ignore the part that doesn't fit on the page." And your mind spun with questions. "Can he do that? Does dx really mean something? How and when do you manipulate it? Is this going to be on the test?"
to both sides of an equation, or saying "we can ignore the part that doesn't fit on the page." And your mind spun with questions. "Can he do that? Does dx really mean something? How and when do you manipulate it? Is this going to be on the test?"
The answer to the last question, I'm afraid, is yes. Understanding what dx actually means is not just something you do to feel philosophically pure. There are certain problems where you really need to understand dx: not to take a derivative or an integral, but to figure out what derivative or integral to take! So there is your motivation for sifting through the rest of this paper. By the time you're done, I hope you will have a pretty good understanding of what dx actually means, and be somewhat ready to start applying your understanding to solve problems.
Now, when you have a quantity whose value is virtually zero, there's not much you can do with it. 2+dx is pretty much, well, 2. Or to take another example, 2/dx blows up to infinity. Not much fun there, right?
But there are two circumstances under which terms involving dx can yield a finite number. One is when you divide two differentials; for instance, 2dx/dx=2, and dy/dx can be just about anything. Since the top and the bottom are both close to zero, the quotient can be some reasonable number. The other case is when you add up an almost infinite number of differentials: which is kind of like an almost infinite number of atoms, each of which has an almost zero size, adding up to a basketball. In both of these cases, differentials can wind up giving you a number greater than zero and less than infinity: an actually interesting number. As you may have guessed, those two cases describe the derivative and the integral, respectively. So let's talk a bit more about those, one at a time.
To start off, remember how you define the slope of a line. You take any two points on the line, and define the slope of the line as Dy/Dx: the change in y divided by the change in x, or "the rise over the run." The slope physically represents how fast the graph is going up. The great thing about lines is, it doesn't matter where you pick your two points, the slope will always be the same.
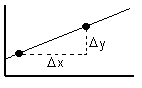
Now, when you want the slope of a curve, you might try to define it the same way. The problem is, the slope varies from point to point. In the curve below, I have labeled three points; and you can see that if we calculated Dy/Dx from A to B we would get a negative slope, from B to C would give us a positive slope, and from A to C might give us zero!
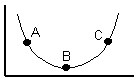
So it's meaningless to talk about "the slope" of that curve. On the other hand, you can certainly talk about the slope at A: it's going down. To quantify this idea, we might pick two points relatively near A—one just above, and one just below—and calculate Dy/Dx on those two points. The closer those points are to A (and to each other), the more accurately they would describe the slope at that point.
So, we're going to invoke a limit, to get "infinitely close" to A. We will talk about Dy/Dx at points very close to A and see what happens to that ratio when Dx approaches 0. Dy also approaches 0, of course, and the ratio of these two tiny numbers approaches the exact slope at that point.
Since we now have differential intervals (that is, they approach 0), we designate them with a d instead of a D. So we have…
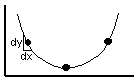
The slope is given by the fraction dy/dx, which is how you have always written the derivative. But now you see that this is not just an arbitrary notation; it is actually a fraction, just as it appears. This may also help explain the chain rule: when they say dz/dx = dz/dy * dy/dx, they really are just multiplying fractions!
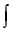 part, which looks like an elongated "S". In fact, that's kind of what it is: it stands for sum, as in adding things. In particular, it means you are adding a virtually infinite number of things. Of course, if the "things" had finite values, that would always give you an infinite answer. But the things are our differential values—each one is roughly zero by itself—so they can actually add up to a reasonable finite number. Whenever you see
part, which looks like an elongated "S". In fact, that's kind of what it is: it stands for sum, as in adding things. In particular, it means you are adding a virtually infinite number of things. Of course, if the "things" had finite values, that would always give you an infinite answer. But the things are our differential values—each one is roughly zero by itself—so they can actually add up to a reasonable finite number. Whenever you see 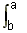 you should assume that you are about to add up an infinite number of differential-sized things.
you should assume that you are about to add up an infinite number of differential-sized things.
So to start with, consider everybody's favorite integral problem, the area under a curve. Just for fun, let's look at the same curve we had above, and think about the area under A-to-C.

Now, if this were a rectangle, we could find the area easily: the area equals the width times the height, and you're done. The problem is, the darn height keeps changing on us, as we move from A to C.
So in order to minimize this problem—the problem of the height changing all the time—we're going to focus on a very small region of the graph, where the height is relatively stable. Start by picking a point x somewhere in our graph, and another point just beyond it: x+dx. Drawing vertical lines at these two points, we get a little region, shaded dark in the drawing below.
If we treat this region as a rectangle, its area is trivial to compute. The height is f(x) and the width is dx. Of course, you can see that the region isn't a rectangle, and the height is only f(x) at the far left. But as dx becomes smaller—as we bring the right side toward the left—the height change becomes less significant, and the region more closely resembles a rectangle. As dx approaches zero, this approximation becomes perfect: the area of the shaded region is f(x)dx.
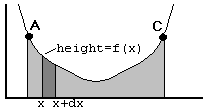
So if the area of that region is f(x)dx, what is the total area under the curve between A and C? Clearly, it is the sum of the areas of all the regions between those two points. And that is what the integral means: in this case, 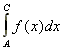 means we add up all those little regions between A and C.
means we add up all those little regions between A and C.
Of course, you already knew that. Without understanding what dx or  means at all, you knew that the integral would give you the area under the curve. So let me move on to a problem that you can't figure out without working pretty directly with dx.
means at all, you knew that the integral would give you the area under the curve. So let me move on to a problem that you can't figure out without working pretty directly with dx.
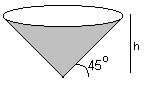
You're not allowed to look it up: all you know is that the area of a circle is pr2. Because the cone goes up at a 45o angle, you can see that the radius of the circle at the top is h, the height of the cone. But what is the volume?
The general way to solve problems like this is to break the object up into small differential chunks. In this case, the chunk would be a circular disk, at a distance x from the ground. The height of the disk is a differential dx.
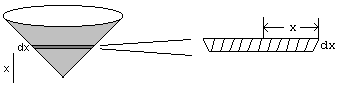
As we did in the area-under-the-curve problem, we're going to make a key approximation here. The width of the disk is not uniform: it is wider on top than on the bottom. But as dx approaches zero, this difference becomes irrelevant, so we are going to treat this region as a uniform circular disk. At that point, finding its volume is not too tough. The radius is x (again, because of our 45o angle, the radius is always the same as the distance from the ground). So its area is px2. Its volume is the area times the height, which you can see is px2dx. As you would expect, the volume is close to zero, since dx itself is so close to zero.
The total volume is an infinite number of those zero-volume disks, added as we go up the disk from x=0 at the bottom to x=h at the top. So we have reached the point where we want to sum up an infinite number of differential amounts, which is when we integrate. The equation is 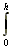 px2dx, which you can work out to be
px2dx, which you can work out to be 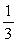 ph3.
ph3.
Of course, there are a lot of things I haven't explained. The biggest one is why you sum up things by taking an antiderivative: maybe I'll write another paper on that some day. But once you do a few problems like this, you will find that a whole world of previously insoluble problems are now within your reach.
|
Important Note Added by Those Wiser Than I
Since I first posted this paper, two different people have emailed me to tell me that Real Mathematicians don't do this. Playing with dx in the ways described in this paper is apparently one of those smarmy tricks that physicists use to give headaches to mathematicians. I didn't even realize I was preaching something nonstandard, because most of my mathematical background comes from physics classes. So, be warned. If you are taking physics classes, the stuff in this paper will be very useful to you. If you are taking math classes, it may help you to gain some intuition, but use it cautiously: you may be expected to master more rigorous methods. Now (I hope you're enjoying this as much as I am) another person wrote, in response to that note, saying: "I noticed a note at the bottom of the page on differentials, saying that Real Mathematicians don't use differentials, that they aren't "rigorous." In fact, a Real Mathematician, Abraham Robinson, in the 1960's proved a rigorous formulation of differentials—a formulation in which you can with full confidence do algebra with infinitely small and infinitely large quantities. It is a branch of mathematics known as "Nonstandard Analysis"; it is actually used by lots of mathematicians because proofs are simpler and theorems less wordy in the "non-standard" formulation. Some people have gone through and written whole introductory calc texts that abandon limits altogether in favor of the much simpler dx, though they get very little attention. There is no shame in using differentials." In all fairness to my earlier critics, I should point out that the first girl who wrote to me told me that I was using "nonstandard analysis," which I thought she meant as a criticism. |
 Gary and Kenny Felder's Math and Physics Help Home Page
Gary and Kenny Felder's Math and Physics Help Home Page
www.felderbooks.com/papers
 Send comments or questions to the author
Send comments or questions to the author