A Bunch of Random Thoughts about Teaching

The problem is not necessarily that he is lazy or stupid or doesn't want to learn. The problem may be that he is practical, and doesn't want to waste his time. Imagine that same kid working for a car mechanic, in a sort of traditional apprenticeship: he makes almost no money, but he earns his keep and learns the trade, and as soon as he knows all about cars, he can strike out on his own and start making some money. I'll bet he would show a lot more enthusiasm for carburetors than he ever does for sonnets! And his enthusiasm would manifest as a better work ethic and a faster learning curve.

Please don't get me wrong, I'm not trying to abandon Shakespeare. I enjoy learning that high-fallutin' stuff. And I also enjoy teaching it, when I have students who actually want to learn. So my motivation here is selfish, to some extent. Every year I have students who are eagerly exploring the pathways of math, and I also have students who are being dragged through the underbrush kicking and screaming, and I would have a lot more fun if I could just focus on the first group.

But there is more at stake here than how much fun Kenny Felder has in class. I don't believe we do anyone a great service by forcing abstract intellectualism on the vast majority of the population who don't need it, don't like it, and don't want it. No one would do that to them when they are adults; why subject them to it while they are teenagers?

My great influence in the world of teaching is my father.

My father, a professor of Chemical Engineering, loves to teach. I have childhood memories of sitting together on the couch as my father taught me math, grammar, and writing. He led me to come to the right conclusions myself, and made me feel smart for figuring them out.

I didn't know that, during the same years that he was teaching me on the couch, my father was also starting to get serious about teaching as a part of his job.

You have to understand that an engineering professor is really an engineering researcher. He gets his Ph.D., does his post-doc, gets a faculty position, gets tenure, becomes a full professor...all based on his ability to do research in engineering. Teaching is a side show to his real job, kind of like Michael Jordan majoring in Geography at UNC—he had to go through his courses, but no one really cares how well he did.

My father went through that whole system, fulfilling all the normal sorts of expectations, until he discovered one day that he was more interested in teaching than in engineering. So he took a radical leap away from engineering research, and started publishing in education journals. He started giving workshops and lectures on how to teach. To any knowledgeable observer, this looked like professional suicide. But along the way, my father came to a few key conclusions.

1. The traditional way that college professors teach is not particularly effective.

2. Great teachers are made, not born. That is, you can be taught how to be a better teacher.

Here is an example of the kind of thing my father explains in his lectures.

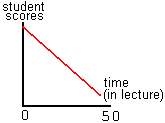
A study was done in which a professor gives a lecture for 50 minutes, and then the students are tested on the contents of the lecture a day or two later. The results of the test are illustrated on the following graph.

It's important to understand what this graph means. On the left side of the graph are the things that the teacher spoke about during the first few minutes of the lecture. As you go from left to right, you are advancing through the 50 minutes of the lecture. Why does the graph go down? Because it's very difficult for students—even bright, well-intentioned, highly motivated students—to pay good attention to a lecture for 50 solid minutes. The graph tells us that the students absorbed and remembered the first few things the professor said, but by the end of the lecture, they were absorbing almost nothing.

Now, we change the lecture slightly. Twice, during the course of the lecture, the professor stops talking and asks a question. It may be a question with a straightforward answer ("What is the next step?" or "What did I do wrong there?") or something more open-ended ("Could there be a more efficient approach?") He asks the students to discuss the question in pairs, with the people they are sitting next to, for one minute. So, for a brief moment, all the students are engaged in thinking and talking. Then the professor continues the lecture. If he does this twice, he has used up an extra 3 minutes of class time or so.

The result? Now the graph looks like this.

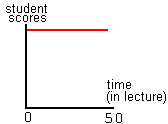
The students are able to pay attention from beginning to end, and they still retain the information days later.

I don't find this experiment particularly surprising. I've watched my own attention span wander when I was forced to attend meetings, and even deliberately woken myself up by asking a question. But hearing about this experiment definitely caused me to change my teaching style.

I mention all this for two reasons. First, I think it is interesting in itself. Second, I think it is a great illustration of everything I said earlier about my father: the reliance on data, the idea that traditional teaching methods are not as effective as one might suppose, and most importantly, the idea that teaching is a skill that can itself be taught and learned, not a knack that some people are magically born with.

Here's another lesson you can draw from that last experiment.

The usual alternative to lecturing is asking the class, "Can anyone suggest the next step?" Three hands go up—the same three hands every time, of course—and the rest of the class is as passive as ever.

On the other hand, if you ask the class to work together in pairs or groups of three, you get almost everyone thinking and talking and writing and problem-solving.

In my Algebra II classes, I use that technique all the time.

Here's a very math-specific question: why do we graph things? When we take a bunch of numbers or functions and draw them on a cute little x-axis and y-axis, with little lines and such, we are not adding any information that was not already present in the numbers or functions themselves. So why do it?

Answer: because you (personally) are very bad at dealing with numbers, but a huge amount of your brain is dedicated to visual pattern recognition. Given a list of numbers, you have a hard time seeing if they are trending up or down; on a graph, you can recognize even a subtle trend immediately. If I tell you that "a quadratic equation can have two solutions, one solution, or no solutions," you probably have to take my word for it; if I tell you that "a line can intersect a U-shape in two places, one place, or not at all," it's kind of obvious.

So graphing is really not about math at all, but about psychology. It's taking advantage of the natural strengths of the human mind.

If you have attended both high school and college, you know that the teaching styles tend to differ dramatically. Of course I am generalizing here, but for the most part, I think you find that college professors are more prone to just drone on for 45 minutes; high school teachers are more likely to come up with active exercises that get the students engaged in talking, thinking, and doing. So that's a point for the high school teachers.

On the other hand, high school teachers also tend to view their students as a lower form of life. They talk down to them in the most condescending tones. If a college student is 30 seconds late to class, he slips in quietly and tries not to disturb anyone; a tardy high school student, on the other hand, is told that he is obviously up to no good, and dealt with accordingly. High schools spend more time and effort being day care providers, or prison guards, than they spend actually imparting knowledge. That's a point for the colleges.

Which difference is more important? For me, there's no contest. As a student, I absolutely despised high school, and I loved college. And no, it was not because I got older and matured over my 19^th summer; it was because they stopped treating me like that.

Many current theorists believe that you should not segregate students by ability. The mentally disabled students, the regular students, and the gifted students, should all be thrown together in the same class. This used to be called "mainstreaming." It is now called—I swear I am not making this up—"differentiation," presumably named by the same people who called the MX Missile the "Peacekeeper."

As you can probably tell from my snide tone, I'm not a fan of this theory. I have taught classes full of standard kids, substandard kids, and gifted kids. They are very different populations with very different needs.

The struggling kids are terrified of math. For years, it has been completely beyond their understanding. They need everything to be concrete as opposed to abstract, meaningful as opposed to useless, and above all, they need success: they need to be able to say about something, almost anything, "Yes, that really makes sense to me." Don't ask them "what is 1/2 - 1/3"; instead, "Here in front of you is a measuring cup filled to the 1/2 level, and here is an empty measuring cup. If I pour from the half-full one into the empty one until the empty one says it is 1/3 full, how much will be left in the other one?" If they can walk away feeling like "I understood one thing today," then maybe tomorrow they can understand two. Maybe math can become OK.

The gifted kids are bored of math. For years, it has been rote, repetitive, and thoughtless. They need challenges. "If a store sells shirts for $10 each, but advertises a buy-two-get-the-third-one-free sale, how much are you actually paying per shirt?" It's OK if they can't figure it out (which may not be OK for the struggling students); if they feel like they can think about it, talk about it, and take delight in the solution, then math can become fun.

Throw them into a class together, and what happens? The class runs at the pace of the low-to-middle-end. The slowest kids are lost, and the upper kids are bored.

My mother and I are both math teachers at the same high school. I am a good teacher; my mother is a great teacher.

What's the difference?

I'm good at explaining math. I offer clear explanations of difficult concepts; I invent exercises that enable my students to figure out the math themselves; I help people see that math is not just a collection of arbitrary rules to follow, but an application of your own common sense. Good teacher.

My mother sees every student in front of her as a full human being—and the students know it. They feel cared about and respected. They tell her the things that they can't tell their parents. They keep in contact with her for years later, because she is the adult they connected with at a time when they needed it, and that changed their lives. And oh yeah, she also taught them a bunch of math.

That's what a great teacher does. I hope everyone has the good fortune, at some point in their education, to have one teacher like my mother.

It amazes me that not only are you a GREAT teacher, but you don't even realize it. I never even liked math until I was in your class. Your teaching style encourages students to want to know more and to believe that they can learn something that would otherwise be too difficult. In my book that makes you an awesome teacher. I've never been taught by your mother, but I would guess you are much more like her than you even realize. :)

I'm particularly touched that you would say that, Vanessa. Because truthfully, you're one of the very few students that I feel like I really have connected with on a level that goes deeper than the math. That has always meant a lot to me, and it still does.

I don't buy that argument. I think a 15 year old who is determined to be a hairdresser is unlikely to ever need trigonometry, can pick it up later if she ever does need it, and perhaps most importantly isn't going to learn it in any useful way if it's forced on her anyway. However, I can't completely dismiss the logic of it. I tend to think that elementary school children should be forced to learn their multiplication tables, even if they adamantly insist that they don't want to do anything in life that requires them to know them. So while I buy the argument "No one would do that to them when they are adults; why subject them to it while they are teenagers?" I do so because of a complex set of beliefs I have about teenagers. Substitute the word "children" for teenagers and I don't buy it anymore, and I don't think there's a hard and fast line that separates the two. I would in some ways be more paternalistic towards 5 year olds than 10 year olds, even less so to 15 year olds, and even less so to 30 year olds, or at least mentally competent ones.

I was saying to Mommy yesterday that I am aware of how politically incorrect the word "tracking" is. I think I can cite all the arguments against it, chapter and verse, and the thorny questions it poses. When do we track? How do we decide how to track? What happens to the late bloomers, who get tracked low, early? What about those with disadvantaged backgrounds? They are all good questions and good arguments, and I can't resolve or refute any of them. And yet, I am willing to insist vehemently that the correct solution is not what we are doing right now; and furthermore, that some tracking system, flawed and mistaken though it would be, would nonetheless be a big improvement.

As for tracking, I basically agree with you on the issues. I think the current system is deeply flawed and a system that tracks too severely is extremely dangerous for all the reasons you just said. So yes, something needs to change, but it should not go to the model that many countries use where a test you take at 11 years old locks you out of a high end career for life. There's got to be a middle ground where you segregate on ability but have some meaningful possibility of shifting up and down. And segregation doesn't have to be an all or nothing proposition. At the extreme end, you could obviously have a range of students all taking the same driver's ed course together, but even in less obvious cases you could have two students that clearly belong in different math classes but in the same English course, or even in reversed positions in their English courses.

Some parents (but probably not most of them) are lucky enough to get appreciation from their grown children; a few are privileged to hear expressions of admiration; and vanishingly few ever see or hear words like yours in this essay. I've earned far more than my fair share of recognition in this life, but none of it could ever mean nearly as much as knowing that you, Elena, and Gary value me and my work, and I can't imagine an expression of that valuing that I would treasure more than this. Thank you.

The "Peacekeeper" was actually a very apt name for the LGM-118A missiles when their program was initiated. See en.wikipedia.org/wiki/Mutual_assured_destruction.

Regarding Shakespeare...if the goal is to "learn to read texts that are written in language that is different than day-to-day language," and if it is true that "service manuals are written in language just as obscure as Shakespeare," then why can't we achieve the same goal with service manuals? Personally, I would rather read Shakespeare. But many students—I would even say "most"—will be more engaged, more committed, and have more fun, if they feel that what they are doing has practical use. And we teachers would be spared the agony of trying to force people who hate Shakespeare to read it and discuss it anyway.

 Send comments or questions to the author